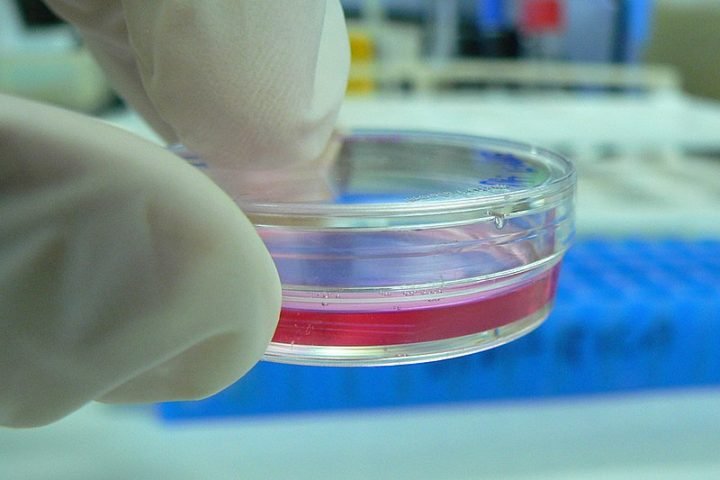
Les processus de ramification immortels sont des processus de ramification où au moins un nouvel individu remplace chaque individu avant la mort.
Les chercheurs ont mis en avant l’immortalité en affirmant que soit
- Une seule particule ne peut pas mourir ; OU
- Il existe une cellule souche immortelle qui donne naissance à des cellules normales qui peuvent ensuite subir une ramification critique.
Le processus de ramification immortelle (IBP) a été discuté dans le document de recherche de PL Krapivsky & S. Redner intitulé « Processus de ramification immortelle » qui constitue la base du texte suivant.

Crédit image: kaibara87 via Wikimédia(CC BY 2.0)
Importance de cette recherche
L’aspect dynamique de la ramification immortelle est discuté dans le document de recherche. Comprendre les processus de ramification immortelle (IBP) pourrait avoir des applications critiques telles que le contrôle des épidémies. Une analyse mathématique permettrait aussi de mieux outiller nos amis de la fraternité médicale pour lutter contre la dengue, le cancer, etc.
Examinons quelques cas d’utilisation courants de la construction d’un modèle mathématique pour étudier le branchement :
- Modéliser et contrôler les épidémies: Par exemple, comprendre les mathématiques derrière Covid-19 peut nous aider à prédire les vagues et à sauver des vies humaines en général.
- Surveillance de l’état des patients: Lorsqu’un patient est touché par le virus de la Dengue, le système auto-immun de l’organisme détruit les plaquettes. Le corps crée également des plaquettes en même temps. La numération plaquettaire chez le patient à un moment donné pourrait être modélisée en comprenant les deux forces ci-dessous :
- Épuisement des plaquettes : le système auto-immun détruit les plaquettes
- Addition de plaquettes : Le corps produit naturellement des plaquettes.
Comprendre l’état actuel du patient (numération plaquettaire) et les deux facteurs ci-dessus peut nous aider à modéliser les besoins en plaquettes du patient qui pourraient être essentiels pour sauver la vie du patient.
La percolation pour comprendre le branchement
Les chercheurs ont dédié ce document de recherche à la mémoire de leur cher ami, Dietrich Stauffer, dont la contribution majeure a été dans le domaine de la percolation. La percolation peut nous aider à étudier les croissances démographiques, la propagation des épidémies, etc.
P → P + P ….. taux r
L’équation ci-dessus illustre que P donne naissance à P + P au taux r. Veuillez noter que P peut faire référence à des cellules, des individus infectés, etc.
Les 3 cas suivants peuvent se produire, en fonction de la valeur de r
- Processus de branchement critique : Dans cette ramification, r=1 signifie que les particules donnent naissance à une seule progéniture avant de mourir. Dans cette branche, la population moyenne est constante dans le temps.
- Branchement sous-critique : Ici, r<1 signifie qu'il y a plus de décès que de naissances. Dans ce cas, la population s'éteint rapidement.
- Branchement supercritique : Ici, r>1, ce qui signifie qu’il y a plus de naissances que de décès. Il en résulte une croissance illimitée.
Les chercheurs ont expliqué les possibilités et dérivé des équations mathématiques pour la ramification critique, la ramification sans extinction et la ramification avec une entrée en détail dans le document de recherche.
Conclusion
Selon les mots des chercheurs,
Nous avons analysé deux processus de ramification immortels (IBP). Le premier est une simple extension de ramification critique dans laquelle l’extinction ne peut pas se produire. Les comportements émergents sont remarquablement subtils, remplis de corrections logarithmiques. Le second est un processus de branchement avec un apport constant de cellules, ou de manière équivalente, l’immigration. Un tel apport constant survient dans une variété de processus à plusieurs corps hors équilibre, tels que l’agrégation avec un apport constant de monomères, la fragmentation avec un apport constant de grands amas et la turbulence avec un apport constant d’énergie à grande échelle. Dans ces exemples, de nombreuses nouvelles fonctionnalités ont été découvertes en incorporant une entrée régulière. Des comportements riches se produisent également dans des systèmes spatialement étendus avec une entrée spatialement localisée et le rôle des degrés de liberté spatiaux dans les IBP pose des défis intéressants.
Source : PL Krapivsky & S. Redner’s “Processus de ramification immortels”